遺伝的アルゴリズムとは? 仕組みや応用例を理解しよう!

はじめに

遺伝的アルゴリズムという言葉を聞いたことがあるでしょうか?

遺伝的アルゴリズムとは、生物の進化からヒントを得た最適化のためのアルゴリズムの一種です。

株の自動取引や工場での製品生産といった、経済学や工学での様々な問題に応用されています。

この記事では、まず、遺伝的アルゴリズムの仕組みや特徴、応用例について説明します。

その後に、社会で生活していくうえで、遺伝的アルゴリズムの考え方をどのように生かすことができるのかということに関して、私の考えを説明します。

遺伝的アルゴリズムの手順

遺伝的アルゴリズムがどのような手順で解を求めるのか簡単に説明します。

遺伝的アルゴリズムは次の図のような手順により行われます。

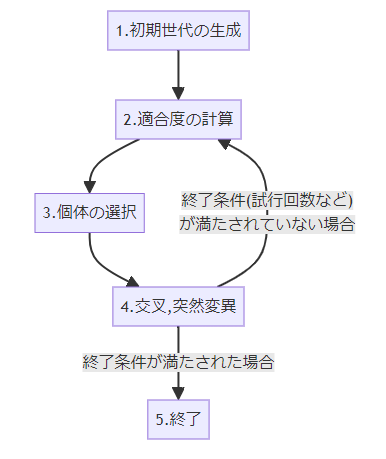
それぞれの世代の個体数をNとします。

初期世代の生成

まずはN個の個体をランダムに生成し、N個の個体全体からなる初期世代を作成します。(最初の時点ではこの初期世代を現世代と呼びます。)
それぞれの個体は、数字やアルファベットで表現された遺伝子が複数個並んだ染色体をもちます。

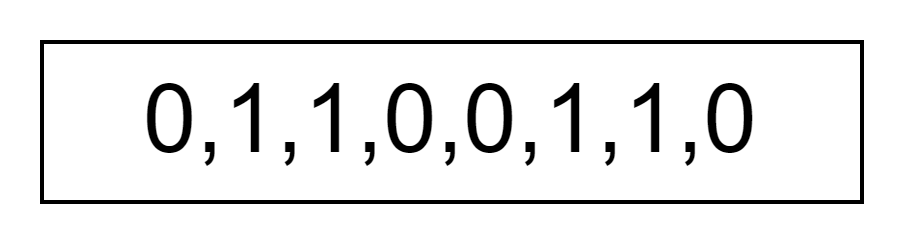
適合度の計算

評価関数によって、適応度の計算を各個体の染色体に対して行います。適応度はそれぞれの個体が環境に適応している度合いを表しています。

選択

環境に適応した個体は次の世代で個体数を増やし、適応しない個体は減らすように、現世代での個体から適合度の高い個体を残す操作を行います。
選択の方法には、適合度に比例した確率で個体を選択する「ルーレット方式」、適応度の順位に基づいてあらかじめ各個体を選択する確率を決めておく「ランキング方式」などがあります。

番号	適合度	選択確率
1	0.1	10%
2	0.2	20%
3	0.1	10%
4	0.3	30%
5	0.3	30%

交叉、突然変異

選択した個体に対して、2つの個体を選んで新しい個体を生成する「交叉」、一定の割合の個体に対して染色体の一部の遺伝子を変化させる「突然変異」といった操作を適用することで次の世代を作成します。

新たに作成した世代を「現世代」として古い世代と置き換えて2の操作に戻ります。

このように、2~4の「適応度の評価」、「選択」、「交叉、突然変異」といった手順を現世代に対して適用することで次の世代を生成し、生成された世代が次の現世代となり、今度はこの新たな世代に対して、2~4の操作を再び適用して新たな世代を生成する…という操作を繰り返します。

その結果、適合度の高い個体がより多くの子孫を残すことで徐々に集団全体が良くなっていくというのが、遺伝的アルゴリズムの考え方です。

遺伝的アルゴリズムの応用例

パラメータを遺伝子とした「個体」として解の候補を表して、複数の解の候補の中から最適な解を見つけるという形で、遺伝的アルゴリズムは様々な分野の問題に対して応用されています。

応用例1 オプション取引

オプションとは「将来のある時点で、特定の価格で原資産を取引する金融商品」を表しています。ここで、原資産とは株や債券などのオプションのもととなる金融商品を表しています。
国内では、日経平均株価を原資産とした日経225、TOPIX（東証株価指数）を対象としたTOPIXオプション取引が代表的です。

オプションの価格を計算するために、まず原資産が従うモデルを考えます。

様々なモデルが存在しますが、ここでは次のようなHestonモデルというモデルを考えます。

Hestonモデル

上の式で出てくるパラメータσ, κ, θ, ρと時点0でのν_tの値を市場のデータを使って適切に定める必要があります。

このように、市場のデータからモデルのパラメータを決定することをキャリブレーションとよびます。

キャリブレーションでは、遺伝的アルゴリズムを以下のように適用することができます。

最小化をする目的関数を

すなわち、市場価格とモデルによって算出された価格の(相対)誤差を最小化するパラメータを遺伝的アルゴリズムによって探索します。
(参考: Calibration of stochastic volatility models )

この記事の最後で、より基本的な設定での遺伝的アルゴリズムの応用について実装例を載せました。

応用例2 工場の生産計画

工場で製品の製造を行う場合を考えます。

製造する製品を切り替える際には、セットアップ時間とよばれる機械の設定を変更する時間が必要です。

セットアップ時間を最小化しつつ製品在庫を安定させるという問題を解くために、遺伝的アルゴリズムを用いて各製品の生産スケジュールを自動生成するという研究が存在します。

このように、パラメータが大量に存在する場合や、最適化の目的となる関数が複数個ある場合であっても、遺伝的アルゴリズムを使用することができます。

遺伝的アルゴリズムのメリット

数学的な手法や他の探索的アルゴリズムと比較した際に、遺伝的アルゴリズムには次のようなメリットが存在します。

様々な問題に対して適用できる

複数の解の候補を並行的に用いて解を探索するという点が、遺伝的アルゴリズムの特徴として挙げられます。

このため、次のような数学的な手法や従来の探索方法では解を探すのが困難な場合でも、遺伝的アルゴリズムであれば適用できる場合があります。

• 解を求めるために必要なパラメータの数が多すぎる。
• 一つ一つの解の候補を順番に探索していると時間が掛かりすぎてしまう。

ランダム性を持たせることができる

問題に対して最適解を探索する場合に、局所解(狭い範囲でしか最適でない解)にたどり着いた後にそこから抜け出すことが
できなくなってしまうという問題がしばしば発生します。

次のグラフは、最小値を求める場合に、x=3で局所解、x=-2で最適解をとる関数を表しています。

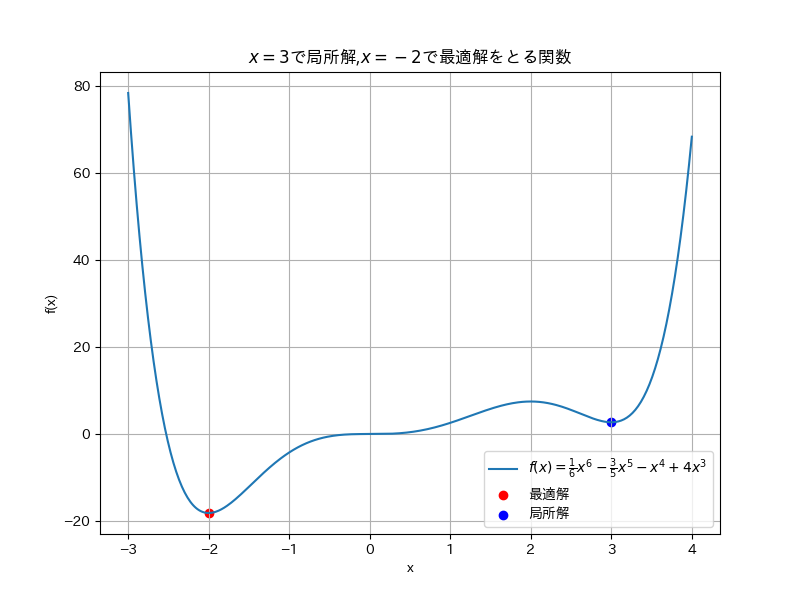
遺伝的アルゴリズムでは、個体の遺伝子の一部を変化させる「突然変異」を行うことでランダム性を持たせ、局所解を抜け出す効果があります。

一方で、「突然変異」を起こす割合である突然変異率をあまり高くしてしまうと、単にランダムに探索している場合とあまり変わらなくなってしまいます。

そのため、通常の場合では突然変異率は低く設定されるようです。

遺伝的アルゴリズムのデメリット

一方で、次のような欠点も存在します。

どのようにパラメータや評価関数を定めるかがはっきりと確立されていない

突然変異率などのパラメータや適合度の計算に必要な評価関数は、進化的アルゴリズムがうまくいくためには非常に重要な要素です。
しかしながら、これらの決め方ははっきりとは確立されていません。

そのため、試行錯誤により職人技的に定めているのが現状のようです。

最適解であることが保証されない

遺伝的アルゴリズムによって求めた解は、常に最適な解であるとは限りません。
例えば、初めのころの世代に非常に適合値が高い個体が存在していた場合には、その個体の遺伝子が急速に全体に広がってしまうことで多様性が失われてしまいます。

結果として、本来の最適な解を得ることができなくなります。

遺伝的アルゴリズムの考え方から得られる教訓

最後に、遺伝的アルゴリズムの仕組みから、私たちが人生を生きる上で次のような教訓を得ることができると考えました。

未知の事柄に積極的にチャレンジすることの重要性

遺伝的アルゴリズムでは局所解の脱出を目標として、「突然変異」によって遺伝子をランダムに変化させます。

人生を生きる上でも、安心して生活することのできる「コンフォートゾーン」に留まるのではなく、未知の事柄に積極的にチャレンジすることが充実した人生を生きる上で重要であると考えられます。

異なるバックグラウンドを持つ人との交流の重要性

遺伝的アルゴリズムにおいては、それぞれの世代の母集団内での多様性を持たせることが最適解を得るために不可欠です。このことから、人生においても異なるバックグラウンドを持つ人との積極的な交流が重要であると考えられます。

状況の変化に対応することの重要性

遺伝的アルゴリズムでは、それぞれの個体がどれだけ現在の環境に適応しているのか表す適応度が重要な指標です。

私たちの生活でも、状況が刻々と変化していく中でどのような行動をとれば周囲の状況に適応することができるか考えることが重要であると考えられます。

まとめ

遺伝的アルゴリズムには次のような特徴があります。

• 生物の進化の過程を模倣したアルゴリズム
• 幅広い問題に活用できる一方、パラメータの決め方が確立されていないなどの課題もある

また、遺伝的アルゴリズムは次のような問題に対して応用されています。

• オプション取引のモデルのパラメーターを決定
• 工場の最適な生産計画の作成

最後に遺伝的アルゴリズムの概念から、私たちが社会を生きる上で次のようなことが重要であると考えました。

• 未知の事柄に挑戦すること
• 異なるバックグラウンドを持つ人との交流
• 現在の状況への適応

参考　ボラティリティのキャリブレーションへの適用例

最後に、BSモデルでのボラティリティのキャリブレーションへの遺伝的アルゴズムの適用例と実装を説明します。

(参考: ON THE CALCULATION OF IMPLIED VOLATILITY USING A GENETIC
ALGORITHM)

まず、BSモデルについて説明します。
時点tでの株価S_tは次のような方程式に従うとします:

ただし、

最小化する目的関数を次のように設定します。

次のアルゴリズムにより、モデルに使用するボラティリティを求めます

実装例

import numpy as np
from scipy.stats import norm

#BS式
def european_option_price(S, K, r, sigma, T):
d1 = (np.log(S / K) + (r + 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
call_price = S * norm.cdf(d1) - K * np.exp(-r * T) * norm.cdf(d2)
return call_price

# 最小化する対象の目的関数：
#予測価格と実際の価格のabsolute error
def absolute_error_function(predicted_price, actual_price):
return np.abs(predicted_price - actual_price)

# 遺伝的アルゴリズムで最適な価格を見つける関数
def genetic_algorithm(S, K, r, T, actual_price, population_size=1000, generations=1000, crossover_rate = 0.1, mutation_rate = 0.05):
# 初期個体群の生成
population = np.random.uniform(0, 1, size=(population_size,))

for generation in range(generations):
# 市場価格との絶対誤差が小さい⇔適応度が大きい　と定める
predicted_prices = european_option_price(S, K, r, population, T)
absolute_error_list = absolute_error_function(predicted_prices, actual_price)

# 選択、交叉、突然変異に用いる個体数
crossover_num = int(population_size*crossover_rate)
mutation_num = int(population_size*mutation_rate)
select_num = population_size - crossover_num - mutation_num

# 選択：適応度が高い(誤差が小さい)個体を残す
selected_indices = np.argsort(absolute_error_list)[:select_num]
selected_population = population[selected_indices]

# 交叉：選択された個体同士を組み合わせて新しい個体を生成
offspring = np.array([np.random.choice(selected_population, 2) for _ in range(crossover_num)])
offspring = np.mean(offspring, axis=1) #2つの親の平均をとって子を作成
# 突然変異：ランダムに個体を変異させる
mutation_list = np.random.uniform(0, 1, size=(mutation_num,))
# 次世代の生成
population = np.concatenate((selected_population, offspring, mutation_list))

last_predicted_price = european_option_price(S, K, r, population, T)
last_error = absolute_error_function(last_predicted_price, actual_price)

# 最適解の選択
last_best_index = np.argmin(last_error)
last_best_volatility = population[last_best_index]
return last_best_volatility

# パラメータの設定
S = 100 # 現在の株価
K = 105 # 行使価格
r = 0.05 # 利子率
true_sigma = 0.3 # ボラティリティ
T = 1 # オプションの満期

# 実際の価格(ここではsigma=0.3のもとでのBS価格を市場価格とする)
actual_price = european_option_price(S, K, r, true_sigma, T)

# 遺伝的アルゴリズムで求められたボラティリティの値
genetic_volatility = genetic_algorithm(S, K, r, T, actual_price)
print("GAで求めたボラティリティ:", genetic_volatility)